Our latest paper, published in Nature Computational Science proposes a unified mathematical and computational foundation for digital twins. Below you can find a high-level summary of our motivation and approach for this work. For technical details check out our full paper (open-access preprint available here), or for a more complete picture of how this work fits into my broader digital twin research check out my PhD thesis.

This work was previously presented at the 2021 AIAA SciTech Forum, and the 2021 SIAM Conference on Computational Science and Engineering.  

Updates:
[January 31 2022] Our paper was selected for the Nature Computational Science one year anniversary collection!
[September 1 2021] This work was featured in a SIAM News article (I am a co-author)
[July 20 2021] This work was featured by Tech Briefs
[July 16 2021] Our MIT News article was featured by the Department of Energy Office of Science
[June 21 2021] This work was featured on Wevolver's The Next Byte Podcast.
[June 15 2021] This work was featured by MIT News! Check out the full story and my interview here.
[May 20 2021] This work was featured by UT Austin News!
[May 20 2021] Our paper was the Nature Computational Science Editor Pick!

A Mathematical and Computational Foundation for Predictive Digital Twins

Current state-of-the-art digital twins are largely the result of custom implementations that require considerable deployment resources and a high level of expertise. In this work we propose a unifying mathematical foundation for digital twins, with the goal of moving from the one-off digital twin to accessible and robust digital twin implementations at scale. Specifically, we define the combined asset-twin system in terms of six key quantities, which are shown in the figure below.

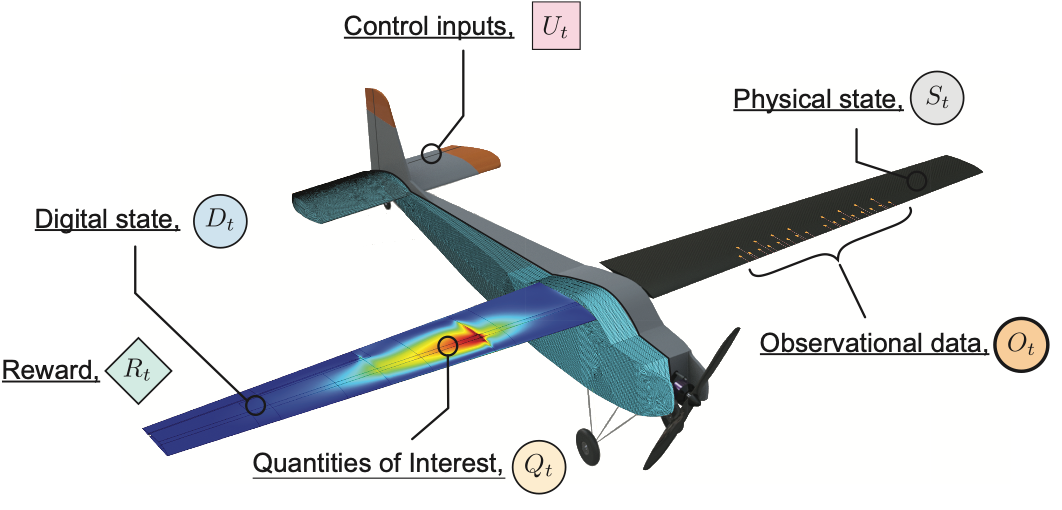
The quantities comprising our mathematical abstraction of the asset-twin system

Defining the system in this way enables us to model the evolution of the physical asset and its digital twin over time. The digital twin learns about the state of the physical asset by assimilating incoming observational data. This information is used to update the internal digital twin models, which are then evaluated to provide accurate analysis and predictions. This enables the digital twin to positively influence the physical asset by informing and/or issuing intelligent control inputs. We model this two-way coupled system using the probabilistic graphical model below, which illustrates the dependencies between quantities in the system as it evolves over time.

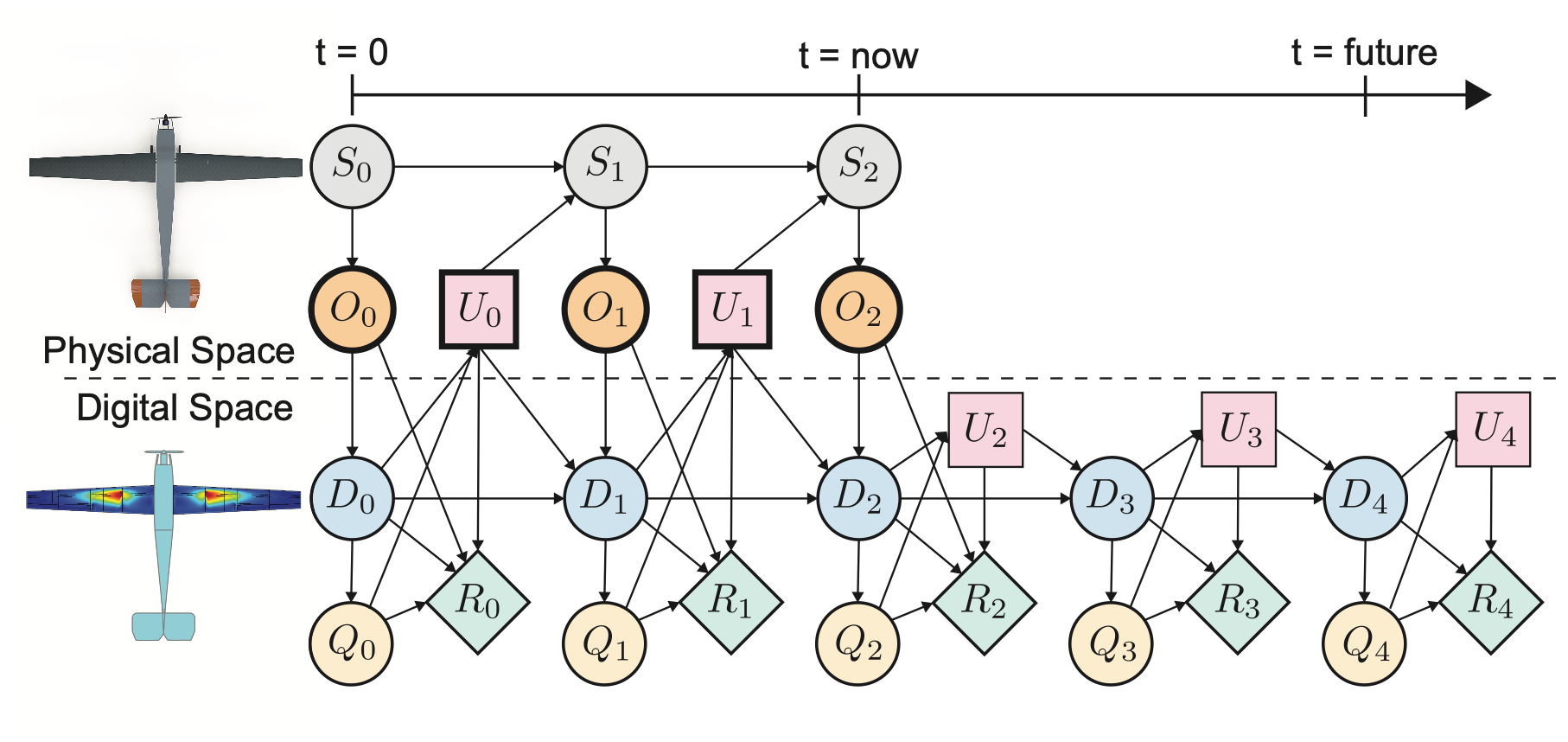
The Probabilistic Graphical Model we propose to model the dynamical evolution of the asset-twin system

Graphical models are a powerful tool for probabilistic representation, inference, and learning, and have been successfully applied in applications ranging from robotics and computer vision, to speech recognition and medical diagnosis. Our proposed probabilistic graphical model serves as a foundation for defining and modeling a digital twin, as well as deriving computationally efficient algorithms for model updating, prediction, and optimal control. More information about the proposed probabilistic graphical model formulation, as well as a demonstration of how we have used the model to perform principled and scalable experimental calibration of a UAV digital twin, can be found in our research paper.