Mathematical and Computational Aspects of Digital Twins:
Application to Self-Aware Autonomous Vehicles

My current research lies at the intersection of computational science and machine learning, with a goal of enabling intelligent autonomous systems. I am particularly interested in the interplay between dynamically updated computational models and real-time sensor data, and how this can enable more intelligent, capable, and effective autonomous systems.
In particular, my PhD research focused on developing methods to enable introspective autonomous aerospace vehicles. These so-called self-aware aircraft are able to detect and assess changes in their structural health, and use this information to dynamically change the way they make decisions. For example, if the aircraft detects damage to a wing, it may choose to fly a more conservative route or abort the mission. This capability has the potential to make autonomous vehicles more safe, efficient, cost-effective, and capable.
This work has been featured by MIT News (this article was also highlighted by the U.S. Department of Energy Office of Science), UT News, the Oden Institute, Tech Briefs, and Wevolver's The Next Byte Podcast.
For more information about this research, check out my complete PhD thesis, my academic publications, or my research blog.
Keywords: Computational modeling, Digital Twin, Data-Driven Reduced-Order Models, Autonomous Systems, Data Assimilation, Bayesian Inference, Machine Learning, Artificial Intelligence, Reinforcement Learning, Probabilistic Graphical Models
Engineering Design Under Uncertainty using Distributionally Robust Optimization
S.M. Thesis project
Advised by Professor Karen Willcox, in collaboration with Professor Andy Philpott.
In this project I studied the role of uncertainty in data-driven engineering design optimization. When designing an engineering system, many quantities that will affect the performance of the system are not perfectly known. Instead, the designer uses data—which is typically subject to randomness and uncertainty—to infer these quantities of interest. For example, the design of a system might depend on certain material properties. To determine these properties we might test many samples of the material, with each experiment resulting in a noisy, uncertain estimate of the relevant material properties. In this work I developed a mathematical formulation and an efficient algorithm for optimizing designs in a way that ensures that the final design is robust to this uncertainty.
For more information, our journal article is available open-access here:
Kapteyn, M. G., Willcox, K. E., & Philpott, A. B. (2019). Distributionally Robust Optimization for Engineering Design under Uncertainty. International Journal for Numerical Methods in Engineering 120.7 (2019): 835-859.
Development of an adaptive-pitch wave energy turbine
Research Internship
Advised by Professor Tsumoru Shintake
In 2014/15 I had a 3 month research internship at the Okinawa Institute of Science and Technology (OIST). During this time I worked under Professor Tsumoru Shintake on the early stages of what is now known as the OIST Wave Energy Project.
During this time we designed, manufactured, and tested a novel design for a wave energy converter: An adaptive-pitch wave energy turbine. The blades of this turbine were designed to be flexible, so that they could adapt their pitch depending on wave strength in order to maximize efficiency protect against strong storm conditions. 
Following my time at OIST, development of the wave energy turbine has continued rapidly. The group now has wave-energy turbines installed on the coast of the Maldives and on the coast of Okinawa!
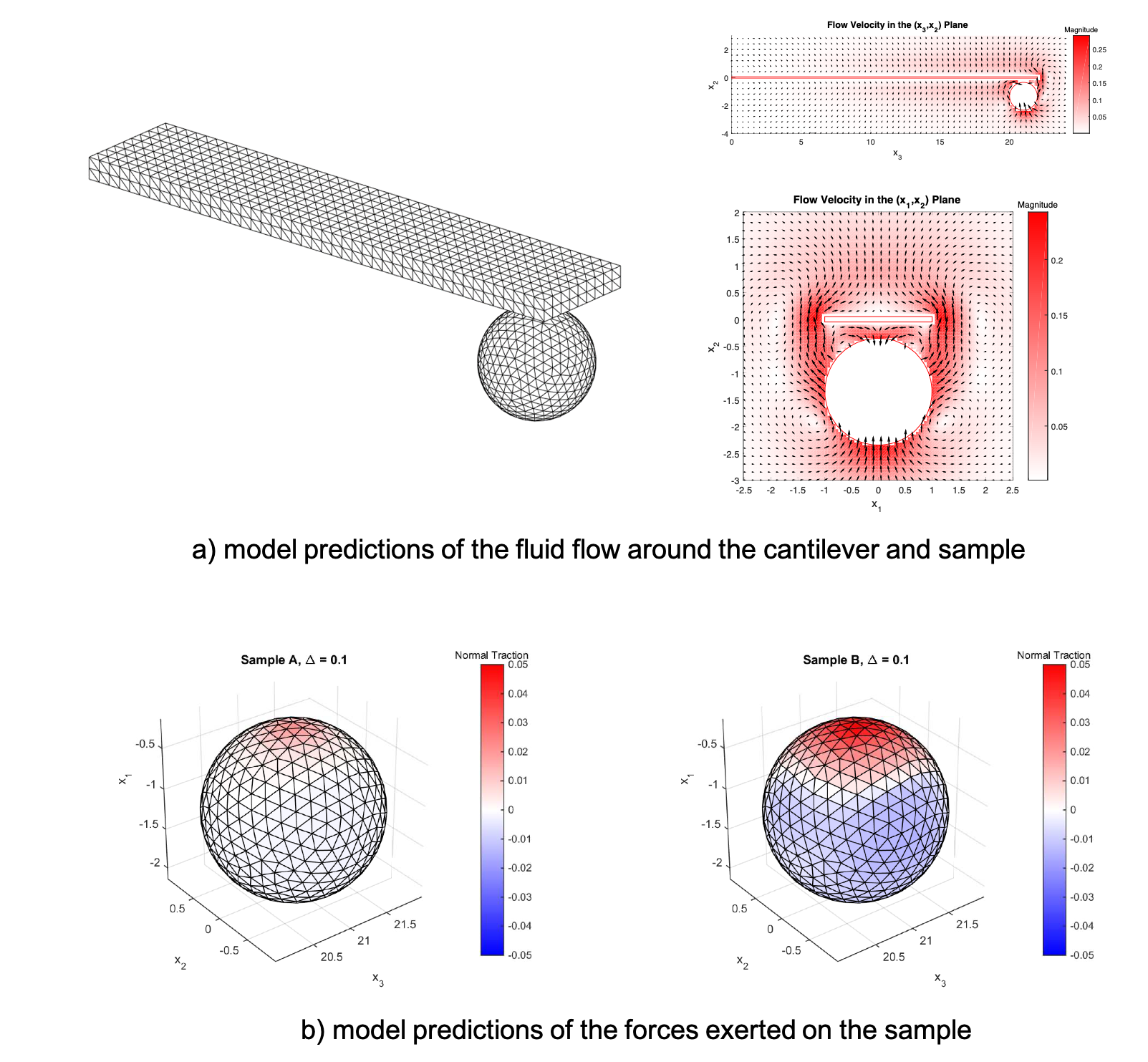
Soft-sensing using microdevices
B.E. (Hons) thesis project
Advised by Dr. Richard Clarke
How do you measure the material properties of a delicate biological cell without damaging it? For my undergraduate thesis project I developed a computational model of the fluid-structure interactions occuring in non-contact atomic force microscopy. The idea is to bring a fluid-immersed microcantilever close to a biological cell, and measure how the oscillation of the microcantilever changes. Based on this we can estimate material properties of the cell. The model utilized the boundary element method (BEM) and was developed in C, using PETSc and MPI.